Partial differential equations (PDEs) are equations involving partial derivatives, modeling diverse phenomena in physics, engineering, and applied mathematics. They describe functions of multiple variables, fundamental in analyzing heat diffusion, wave propagation, and fluid dynamics, essential for understanding complex systems and processes.
1.1. Definition and Overview of PDEs
A partial differential equation (PDE) is an equation involving partial derivatives of a function of multiple variables. It relates the function’s rate of change in different directions, capturing spatial and temporal variations. PDEs describe phenomena like heat diffusion, wave propagation, and fluid flow, making them fundamental in physics, engineering, and applied mathematics. Unlike ordinary differential equations (ODEs), PDEs involve functions of several variables, leading to more complex solutions. The order of a PDE is the highest order of any partial derivative, while its degree is the highest power of any derivative term. PDEs can be linear or nonlinear, homogeneous or non-homogeneous, and their classifications guide solution methods. Understanding PDEs is essential for modeling real-world processes and systems.
1.2. Historical Development and Importance
The study of partial differential equations (PDEs) traces back to the 18th century, with contributions from mathematicians like d’Alembert, Euler, and Fourier. D’Alembert’s work on wave equations and Fourier’s on heat conduction laid foundational principles. These equations became central to understanding physical phenomena, such as sound, heat, and fluid motion. The development of PDEs paralleled advancements in calculus and mathematical physics, driven by the need to model real-world processes. Their importance grew as they provided mathematical frameworks for fields like acoustics, thermodynamics, and quantum mechanics. Today, PDEs are indispensable in engineering, biology, and finance, showcasing their universal applicability and profound impact on scientific and technological progress.
1.3. Motivation and Applications in Real-World Problems
Partial differential equations (PDEs) are motivated by their ability to model complex, multi-variable phenomena in physics, engineering, and applied sciences. They describe processes like heat diffusion, wave propagation, and fluid dynamics, which are crucial for understanding and predicting real-world behaviors. Applications of PDEs include simulating weather patterns, analyzing material stress in engineering, and modeling population growth in biology. In finance, PDEs are used to price options and manage risk. Their versatility and accuracy make them indispensable tools for solving practical problems across diverse disciplines, enabling advancements in technology and scientific research.

Classification of Partial Differential Equations
PDEs are classified as linear or nonlinear, based on their order and degree, and whether they are homogeneous or non-homogeneous, guiding solution methodologies.
2.1. Linear vs. Nonlinear PDEs
Partial differential equations can be classified as linear or nonlinear based on the degree of the unknown function and its derivatives. Linear PDEs exhibit constant coefficients and lack cross-product terms, making them easier to solve using methods like Fourier analysis. Examples include the heat equation and Laplace’s equation. Nonlinear PDEs, however, involve terms where the function or its derivatives are multiplied together, complicating solutions. Navier-Stokes equations and Einstein’s field equations are classic nonlinear examples. The distinction is crucial as linear PDEs often allow for superposition principles, while nonlinear ones typically do not, leading to phenomena like shock waves and solitons. This classification significantly impacts the choice of analytical and numerical methods.
2.2. Order and Degree of PDEs
The order of a partial differential equation (PDE) is determined by the highest order of any partial derivative present. For instance, if the highest partial derivative is of the second order, the PDE is classified as second-order. The degree, however, refers to the highest power to which any derivative is raised. Understanding the order and degree is crucial as they influence the complexity and the methods used to solve the equation. Higher-order PDEs often describe more intricate physical phenomena, such as wave propagation or heat diffusion. The degree, while less commonly emphasized, plays a role in determining the nonlinearity and the potential for singular solutions. Together, order and degree provide a foundational framework for categorizing and approaching PDEs in various applications.
2.3. Homogeneous and Non-Homogeneous PDEs
A partial differential equation (PDE) is termed homogeneous if all terms involve the dependent variable or its derivatives, with no additional independent terms. Conversely, a non-homogeneous PDE includes a term that does not involve the dependent variable, often referred to as a source term. For example, the heat equation with a source term is non-homogeneous, while the Laplace equation is homogeneous. This classification is vital as it influences the solution techniques and the behavior of the PDE. Homogeneous PDEs often admit solutions that can be scaled or combined linearly, whereas non-homogeneous equations require additional methods, such as particular solutions, to account for the source term.

Methods of Solving PDEs
PDEs are solved using classical methods, integral transforms, or numerical schemes, each tailored to equation type and boundary conditions, ensuring accurate and efficient solutions.
3.1. Classical Methods for Linear PDEs
Classical methods for solving linear PDEs include separation of variables, Fourier transforms, and the method of characteristics. Separation of variables simplifies PDEs into ordinary differential equations (ODEs) by assuming solutions in product form. Fourier transforms leverage orthogonality of trigonometric functions for solving equations like the heat and wave equations. The method of characteristics is used for first-order linear PDEs, transforming them into a system of ODEs along characteristic curves. These techniques are foundational and widely applied in physics and engineering, offering analytical solutions for linear PDEs under specific boundary conditions. They are often introduced in lecture notes and textbooks as essential tools for understanding PDE behavior.
3.2. Integral Transforms and Fourier Analysis
Integral transforms, such as Fourier and Laplace transforms, are powerful tools for solving linear PDEs. Fourier analysis is particularly effective for problems with constant coefficients, enabling the transformation of PDEs into algebraic equations in frequency space. The Fourier transform simplifies heat and wave equations by converting partial derivatives into multiplicative factors, facilitating solutions in the frequency domain. Laplace transforms are useful for problems with time-dependent boundary conditions, converting PDEs into ordinary differential equations (ODEs) in the transform space. These methods are widely discussed in lecture notes and textbooks, offering elegant solutions to various physical phenomena, such as heat conduction and wave propagation, by leveraging orthogonality and frequency decomposition.
3.3. Numerical Methods and Difference Schemes
Numerical methods provide approximate solutions to PDEs when analytical solutions are difficult or impossible to obtain. Finite difference methods approximate derivatives using grid-based difference quotients, while finite element methods discretize the domain and solve using variational principles. These schemes are widely used for problems like heat diffusion and fluid dynamics. Stability and convergence analysis are critical to ensure accurate results. Time-stepping techniques and mesh refinement further enhance accuracy. Lecture notes and resources often detail these methods, offering practical implementations for real-world applications, such as engineering and physics problems, where numerical solutions are essential due to the complexity of PDEs.

Applications of Partial Differential Equations
Partial differential equations model various natural phenomena, such as heat diffusion, wave propagation, and fluid dynamics, with applications in physics, engineering, and quantum mechanics.
4.1. Heat Conduction and Diffusion Processes
Partial differential equations (PDEs) are instrumental in modeling heat conduction and diffusion processes. The heat equation, a classic example, describes how heat distributes itself over time in a given region. This equation is derived from Fourier’s Law of Heat Conduction, which relates the heat flux to the temperature gradient. Similarly, diffusion processes, such as the spread of chemicals or particles, are governed by PDEs that account for the movement of substances from areas of higher concentration to lower concentration. These equations are fundamental in physics, engineering, and chemistry, enabling the analysis of thermal management systems, material science applications, and environmental dispersion problems. Solving these PDEs provides critical insights into optimizing systems and predicting behavior under various conditions.
4.2. Wave Propagation and Vibratory Phenomena
Partial differential equations (PDEs) are essential for describing wave propagation and vibratory phenomena in various physical systems. The wave equation, a fundamental PDE, governs how waves propagate through a medium, such as sound waves in air or seismic waves in the Earth. Vibratory phenomena, like the oscillations of strings or membranes, are also modeled using PDEs. These equations capture the spatial and temporal variations of the system, enabling the prediction of wave speeds, amplitudes, and interference patterns. Applications include acoustics, optics, and quantum mechanics, where PDEs provide critical insights into wave behavior and vibrational modes. Solving these equations helps engineers and physicists design systems, from musical instruments to advanced communication technologies, by understanding and controlling wave dynamics.
4.3. Fluid Dynamics and Engineering Applications
Partial differential equations (PDEs) play a crucial role in fluid dynamics and engineering by modeling the behavior of fluids and gases. The Navier-Stokes equations, a set of nonlinear PDEs, describe fluid flow, pressure, and velocity fields, essential for designing pipelines, turbines, and aerodynamic systems. Engineering applications rely on PDEs to analyze heat transfer, stress distribution, and fluid-structure interactions. These equations enable simulations for optimizing industrial processes and predicting system performance under various conditions, making them indispensable for solving complex engineering challenges and advancing technological innovations;
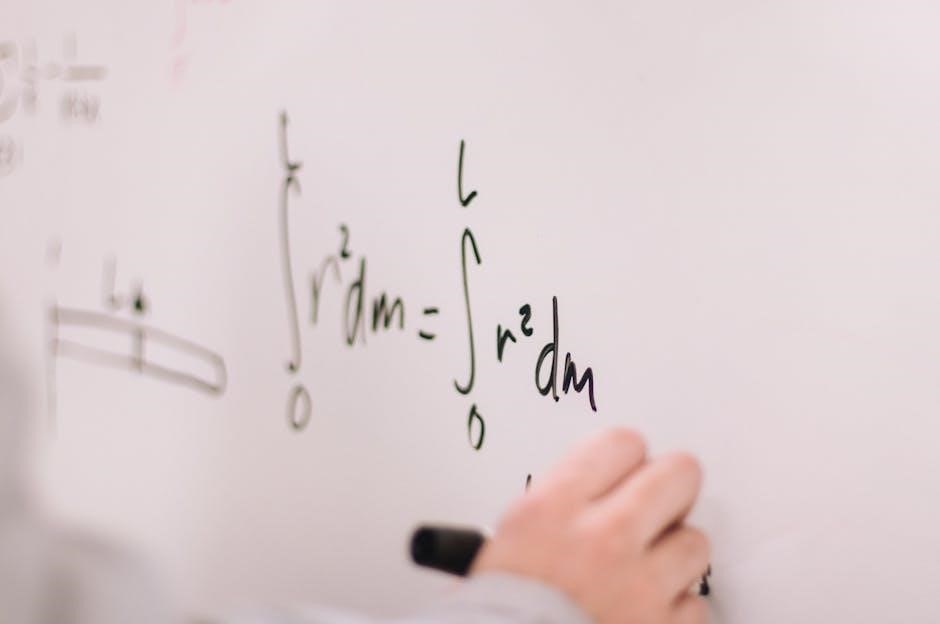
Resources and Lecture Notes on PDEs
Comprehensive resources, including PDF lecture notes from universities like Michigan State and Radboud, cover PDEs, offering theoretical insights and practical applications for advanced learning and research.
5.1. Recommended PDF Lecture Notes and Books
Several high-quality PDF lecture notes and books on partial differential equations are available for comprehensive learning. Lecture notes from universities such as Michigan State and Radboud provide detailed explanations of PDE fundamentals, including classification, methods of solution, and applications. Books like “Linear Partial Differential Equations and Fourier Theory” offer in-depth theoretical insights, while resources from professors like Baisheng Yan cover practical problem-solving. These materials are ideal for both undergraduate and graduate students, offering a balanced mix of theory and real-world examples. They are accessible online, making them invaluable for self-study or supplementary learning. These resources are essential for mastering the core concepts and advanced topics in PDEs.
5.2. Online Courses and Tutorial Materials
5.3. Research Papers and Advanced Topics
Research papers on partial differential equations (PDEs) explore advanced topics such as nonlinear equations, optimal control, and numerical methods. These papers often present novel algorithms and techniques for solving complex PDEs, including difference schemes and maximum principle applications. They also delve into specialized areas like traveling wave solutions for parabolic equations and mixed-type PDEs. Advanced topics in PDE research frequently address theoretical frameworks, ensuring stability and accuracy in numerical simulations. These resources are invaluable for researchers and graduate students seeking to explore cutting-edge developments in the field. They provide detailed insights into modern methodologies and their applications across various scientific domains.



